1.2 二进制代码

在本教程中，我们将学习数字电子学的基本要求之一，即二进制数制的二进制码。一些常见的二进制码包括8421码（BCD）、2421码、5211码、Excess-3码和Gray码。

大纲

• 不同类型的二进制码

第一个成功的电气通信系统是电报，它由塞缪尔·F·B·莫尔斯（Samuel F.B. Morse）于1832年发明。电报操作员使用一种点击声的代码来发送消息。如果按键时间较短，则为莫尔斯电码中的“点”；如果按键时间较长，则为“划”。下面展示了一个莫尔斯电码示例：

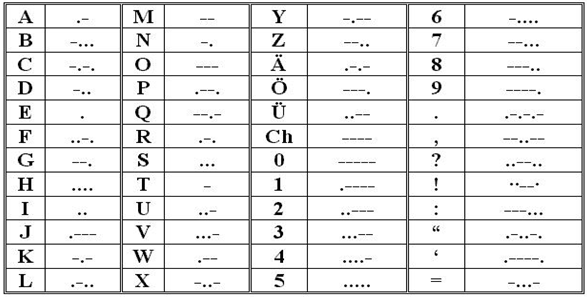
从逻辑上讲，利用上述代码可以写出各种无数组合的点和划，以表示任何单词（甚至句子）。同样地，二进制数字也可以用于生成这种无数的组合，这些组合可以被视为二进制码。

除了常用的8421码（BCD）之外，其他二进制码，如2421码、5211码、反射码、顺序码、非加权码、Excess-3码和Gray码也很受欢迎。

常用二进制码

在深入探讨各个二进制码的细节之前，让我们先快速了解一下一些常用的二进制码。以下是列表：

• 8421码
• 2421码
• 5211码
• Excess-3码
• Gray码

在上述列表中，前三种，即8421、2421和5211是加权二进制码，而其他两种是非加权二进制码。

加权二进制系统

在十进制数制（位值制）中，连续位的值分别为$10^4, 10^3, 10^2, 10^1, 10^0, 10^{-1}, 10^{-2}, 10^{-3}$……从左到右依次递减。很容易理解，十进制数制中数字的权重是“10”。

例如：

$(3546.25)_{10} = 3 \times 10^3 + 5 \times 10^2 + 4 \times 10^1 + 6 \times 10^0 + 2 \times 10^{-1} + 5 \times 10^{-2}$

同样地，二进制数制（位值制）中连续位的值被称为加权二进制系统。二进制系统中的权重从左到右依次为$2^4, 2^3, 2^2, 2^1, 2^0, 2^{-1}, 2^{-2}, 2^{-3}$……很容易理解，二进制数制中数字的权重是“2”。

例如：

$(1110110)_2 = 1 \times 2^6 + 1 \times 2^5 + 1 \times 2^4 + 0 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0$ $= 64 + 32 + 16 + 0 + 4 + 2 + 0 = (118)_{10}$

二进制权重

当出现任何二进制数时，可以按照以下方法轻松找到其十进制等效值：

• 如果某一位上是1，则加上该位的权重。
• 如果某一位上是0，则忽略该位的权重。

例如，二进制数1100的十进制等效值为8 + 4 + 0 + 0 = 12。

8421码或BCD码

十进制数0、1、2、3、4、5、6、7、8、9可以用二进制数表示，如下表所示。所有这些二进制数再次在最后一列中扩展为4位表示。根据加权二进制数字，4位二进制数可以根据从左到右的位值表示为8421（$2^3 2^2 2^1 2^0 = 8421$）。

Decimal Number	Binary Number	4 BIT Expression (8421)
0	0	0000
1	1	0001
2	10	0010
3	11	0011
4	100	0100
5	101	0101
6	110	0110
7	111	0111
8	1000	1000
9	1001	1001

根据上述表达式，所有十进制数都以8421的形式写成了4位二进制码，这被称为8421码，也称为二进制编码十进制（BCD）码。

由于这是一种直接码，任何十进制数都可以轻松表示，因为各个位置的权重是直接的，便于转换为8421码。

除了8421码之外，还有其他不太常见的二进制码，它们可能会让人感到困惑。这些码包括2421码、5211码、反射码、顺序码、非加权码、Excess-3码和Gray码。这些码在某些特定应用中具有其独特的重要性，并且可能对某些特殊应用非常有用。

2421码

2421码也是一种4位应用码，其中二进制权重从左到右依次为2、4、2、1。

DECIMAL NUMBER	BINARY NUMBER	2421 CODE
0	0	0000
1	1	0001
2	10	0010
3	11	0011
4	100	0100
5	101	1011
6	110	1100
7	111	1101
8	1000	1110
9	1001	1111

5211码

5211码也是一种4位应用码，其中二进制权重从左到右依次为5、2、1、1。

DECIMAL NUMBER	BINARY NUMBER	5211 CODE
0	0	0000
1	1	0001
2	10	0011
3	11	0101
4	100	0111
5	101	1000
6	110	1010
7	111	1100
8	1000	1110
9	1001	1111

反射码

可以观察到，在2421码和5211码中，十进制数9的码是十进制数0的码的补码，十进制数8的码是十进制数1的码的补码，十进制数7的码是十进制数2的码的补码，十进制数6的码是十进制数3的码的补码，十进制数5的码是十进制数4的码的补码。这些码被称为反射码。从下表中可以观察到这一点：

Decimal Number	Binary Number	2421 Code	5211 Code
0	0	0000	0000
1	1	0001	0001
2	10	0010	0011
3	11	0011	0101
4	100	0100	0111
5	101	1011	1000
6	110	1100	1010
7	111	1101	1100
8	1000	1110	1110
9	1001	1111	1111

注意：8421码不是反射码。

顺序码

顺序码是指在二进制表示中，两个连续数字之间仅相差一位的编码。8421码和Excess-3码是顺序码的示例。2421码和5211码不属于顺序码。

Decimal Number	Binary Number	8421 Code	Excess-3 Code
0	0	0000	0011
1	1	0001	0100
2	10	0010	0101
3	11	0011	0110
4	100	0100	0111
5	101	0101	1000
6	110	0110	1001
7	111	0111	1010
8	1000	1000	1011
9	1001	1001	1100

非加权码

有些编码并不遵循序列二进制数的权重，这些编码被称为非加权码。ASCII码和Gray码是一些例子，它们是为特定目的的应用而编码的，并不遵循加权二进制数的计算。

Excess-3码

如上所述，有些编码并不遵循二进制权重，Excess-3码是其中的一个例子，它是一种重要的4位编码。一个十进制数的Excess-3码是通过将其8421码加上数字3得到的。

例如，将15转换为Excess-3码，首先需要将每个数字分别加上3，如下所示。

Excess-3码示例

1. 求$(237.75)_{10}$的Excess-3码。
2. 求Excess-3码$110010100011.01110101$对应的十进制数。

解：

1. 求$(237)_{10}$的Excess-3码
   将每个数字分别加上3，即2、3和7分别变为5、6和10。这些数字5、6和10需要转换为二进制形式，结果为$010101101010$。
   求$(.75)_{10}$的Excess-3码
   通过将7和5分别加上3，替换为10和8，即$(.75)_{10}$的Excess-3码为$.10101000$。
   组合整数和小数部分的结果
   $(237.75)_{10}$的Excess-3码为$010101101010.10101000$。

2. Excess-3码为$110010100011.01110101$
   将4位一组分开，等效的Excess-3码为$1100\ 1010\ 0011.0111\ 0101$。
   从每组4位中减去$0011$，得到新的数字为：$1001\ 0111\ 0000.0100\ 0010$。
   因此，对应的十进制数为$(970.42)_{10}$。

Gray码

Gray码是一种编码方式，其中一个数字与前一个数字仅有一位不同。例如，十进制数13和14分别用Gray码表示为1011和1001，这两个数字仅在右侧的第二位不同。同样地，左侧第一位在7和8之间变化，分别是0100和1100，这也被称为单位距离码。Gray码在数字电子学中具有非常特殊的地位。

DECIMAL NUMBER	BINARY CODE	GRAY CODE
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110
5	0101	0111
6	0110	0101
7	0111	0100
8	1000	1100
9	1001	1101
10	1010	1111
11	1011	1110
12	1100	1010
13	1101	1011
14	1110	1001
15	1111	1000

结论

本教程是对二进制码的入门介绍。您学习了不同的二进制码，包括8421码（BCD）、2421码、5211码、Excess-3码和Gray码。